第16章 2Dラジアル法
第15章までは,すべてデカルト座標系におけるサンプリングを行う,いわゆるCartesian samplingによる撮像法の紹介であった.
Cartesian samplingには,静磁場の不均一性や,グラジエントの非線形性が,画像のボケにはならず,画像の歪みにしかならないという大きなメリットがあるが,Cartesian samplingではないNon Cartesian samplingには,そのような性質はないものの,一定の長所がある(後述).
そこで,Non Cartesian samplingの代表例であるradial法とspiral法(Fig.16-1)を,本章と次の章で解説する.
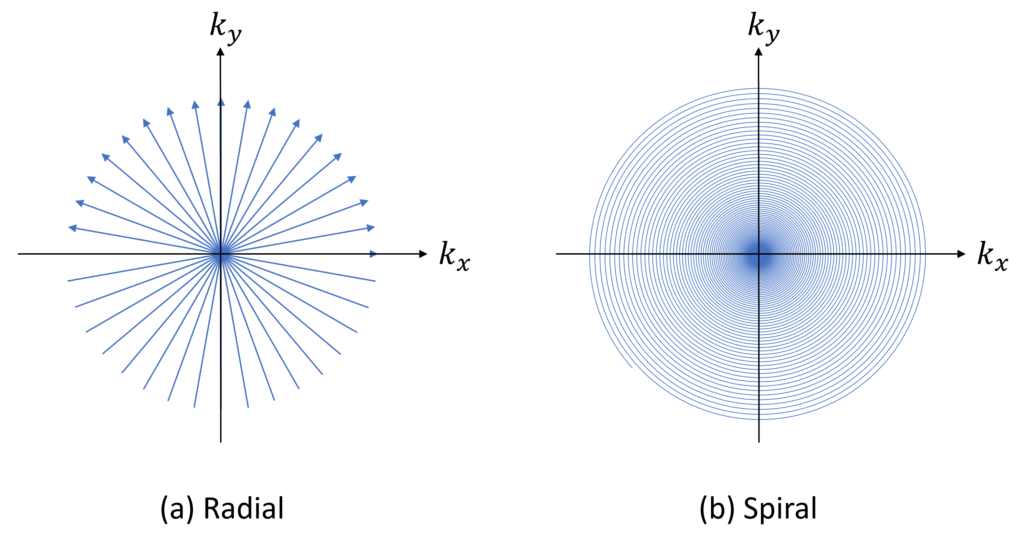
Fig.16-2とFig.16-3に,180°あたりのショット数が200のときのパルスシーケンスチャートを示し,Fig.16-4に,シーケンスのソースコードを示す.
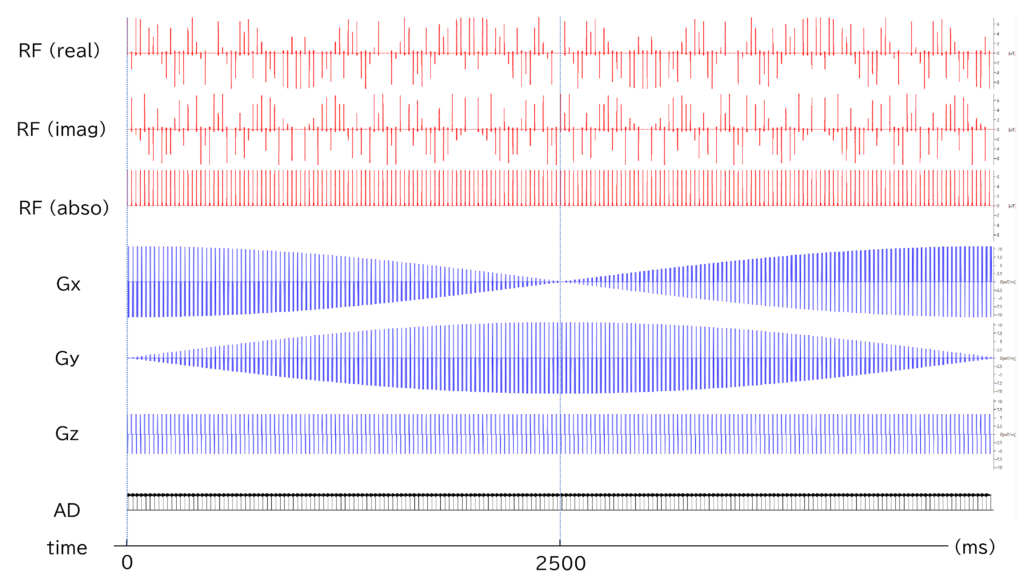
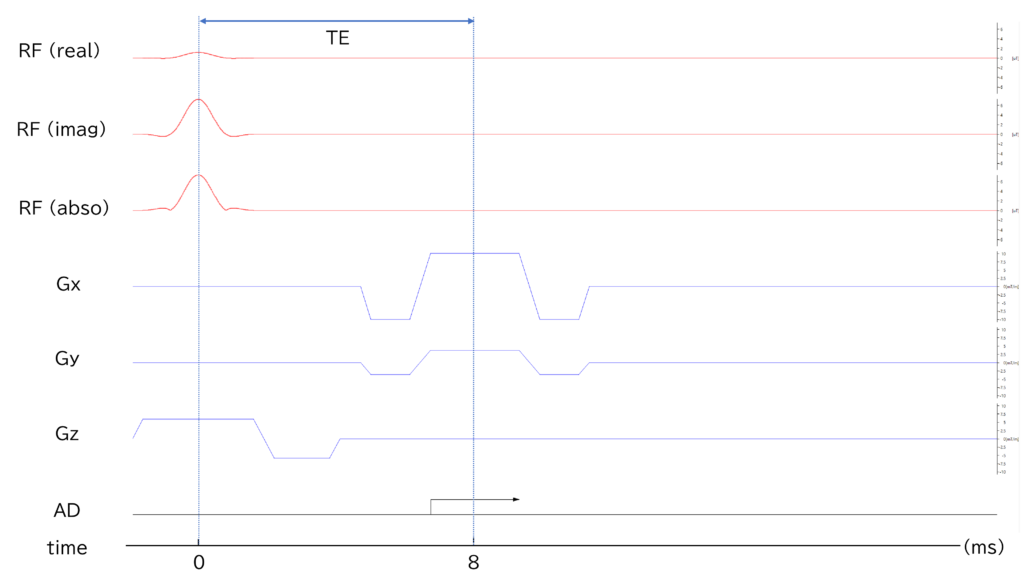

このように,TR=500 msとしてT1強調画像を取得するために,RF spoilingを行い,面内のグラジエント強度を,一つの角度に対するcosine関数とsine関数に比例して同時に変化させている.このようにして,常にk空間の原点を通過するトラジェクトリを実現している.
このように,トラジェクトリがk空間の原点を通る直線であるradial法において,k空間の端のsampling点におけるサンプリングに関するNyquist条件を満たすためには,256×256画素のk空間に対しては,180°あたりのショット数は約400(π/(1/128) = 128π~402)でなければならない.
Fig.16-5に,ショット数を400,200,100と変化させたときの,Bloch simulationにより求めた再構成画像(256×256画素)を示す.TR = 500 ms,TE = 8 ms,dummy数は10とした.このように,ショット数400と200では,ほとんど変化は見られないが,ショット数100では,分解能の低下がみられる.なお,画像再構成には,NUFFTを使用した(Fig.16-7).
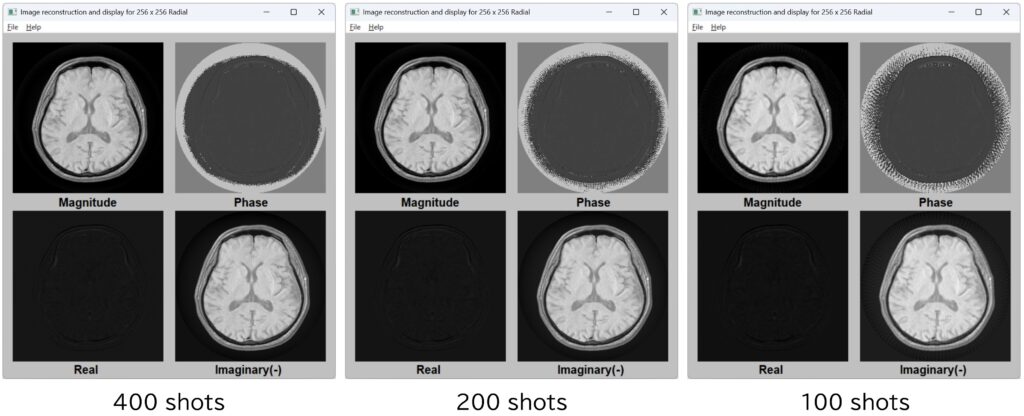
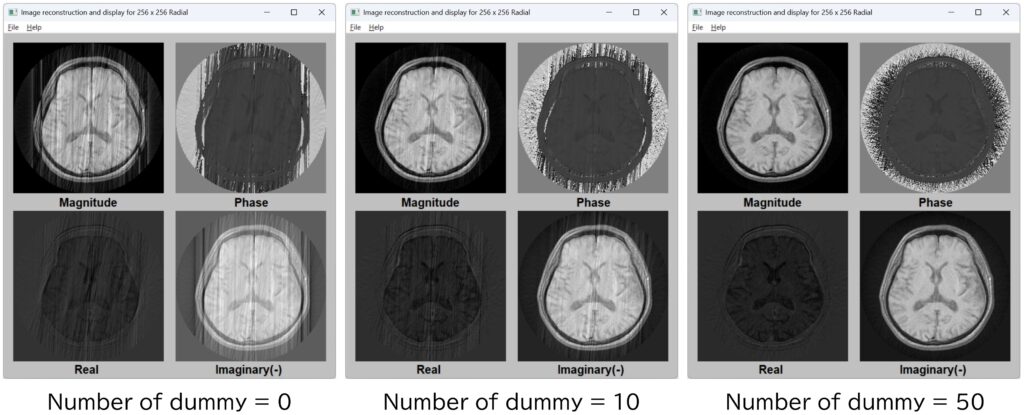
Fig.16-6には,サンプリング開始前のdummyスキャンの回数に依存した,Bloch simulationの結果を示す.TR = 25 ms,TE = 8 ms,ショット数は200とした.このように,k空間の端からサンプリングを行うCartesian samplingに比べ,radial samplingの場合には,最初のスキャンからk空間の原点付近のデータ取得を行うため,核磁化が定常状態に達してからサンプリングを行うのが必須である(Cartesian samplingの場合には,顕著には現れない:もちろん,centric order samplingのときには問題となる).
さて,radial samplingの有用な応用は,非常に短いエコー時間(Ultrashort TE)での撮像であり,このようなシーケンスでは,リフォーカスグラジエントを短くできるSLRパルスによる励起と,その直後のk空間の原点からのradial samplingが行われる.
最後に,上記の画像の再構成に使用した,Non uniform fast Fourier transform (NUFFT)の手法を説明する(Fig.16-6).
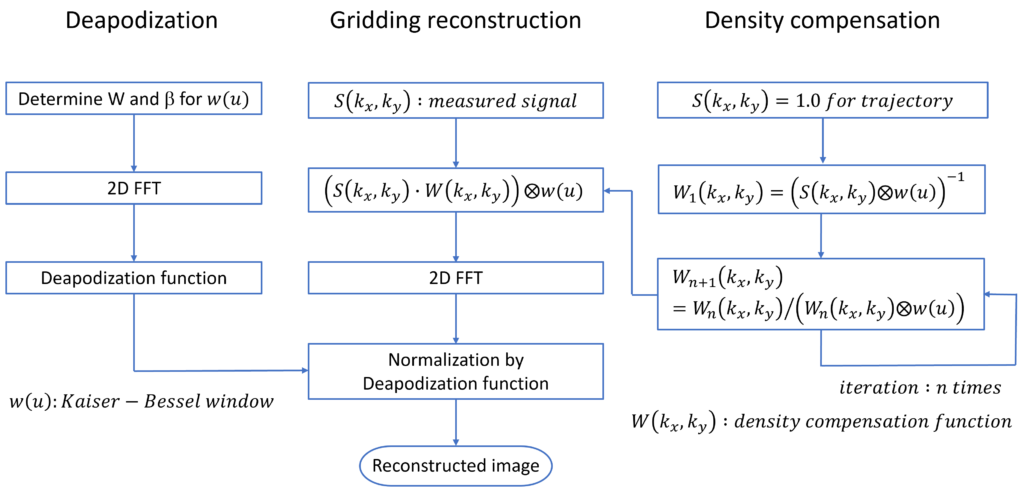
NUFFTは,下の図に示すように,3種類の処理から構成されるが,基本的な考え方は,任意の軌道でサンプリングされた信号データを,ウィンドウ関数(Kaiser-Bessel window)を用いて補間することにより,デカルト座標系の格子点上の信号値を求め,それを2DFFTすることによって再構成画像を求める.この際に,補間演算に伴う画像空間における強度変化の補正(deapodization)と,k空間における軌道の局所的密度に起因する強度補正(density compensation)が必要となる.
Deapodizationでは,Kaiser-Bessel windowを特徴づけるWとβを決め,それに対するウィンドウ関数w(u)を2DFFTすることによって,強度補正のためのdeapodization functionを求める.
Density compensationは,k空間上のトラジェクトリS(kx, ky)のサンプリング点を,1.0という規格化された値で埋め,その関数とウィンドウ関数w(u)をconvolutionすることによって,強度補正関数W(kx, ky)を求める,という操作を繰り返し,精度の高い強度補正関数を求める(10回程度繰り返す).
計測した信号S(kx, ky)は,強度補正関数W(kx, ky)を乗じた上で,ウィンドウ関数w(u)とconvolutionすることで,デカルト座標系の格子点上の信号値を求め,それを2DFFTし,deapodization functionで補正することにより,再構成画像を求める.